About OLPS
Portfolio Selection
Online Portfolio Selection is a research problem dealing with optimal allocation of wealth to a number of assets, in order to meet certain investment objectives (e.g. Maximizing Wealth, Minimizing Risk, etc.).
During the investment phase, at any instance, the historical performance of all assets is available to us, and based on this, we re-balance our portfolio, i.e., allocate all the wealth that we have to all the available assets in some certain proportions.
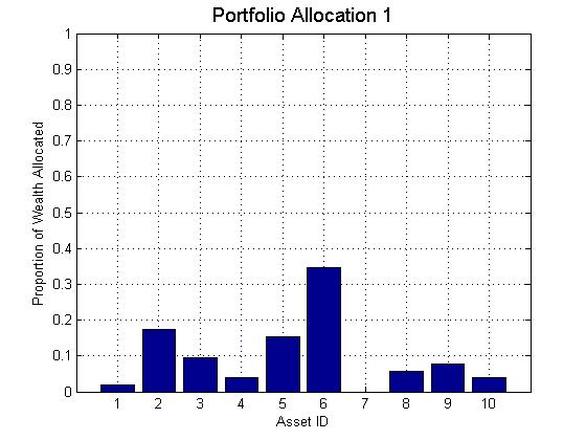
For example, the following graph depicts a portfolio allocation to 10 assets.
Online Portfolio Selection is a research problem dealing with optimal allocation of wealth to a number of assets, in order to meet certain investment objectives (e.g. Maximizing Wealth, Minimizing Risk, etc.).
During the investment phase, at any instance, the historical performance of all assets is available to us, and based on this, we re-balance our portfolio, i.e., allocate all the wealth that we have to all the available assets in some certain proportions.
For example, the following graph depicts a portfolio allocation to 10 assets.
The height of the bar for each stock determines what fraction of the available wealth has been allocated to that particular asset or stock. In the above figure, Asset 6 has the highest wealth allocation at 35%, and Asset 7 has 0% wealth allocation. Naturally all wealth allocations must be greater than 0 and their sum must be equal to 1. (In this problem we do not consider shorting of stocks).
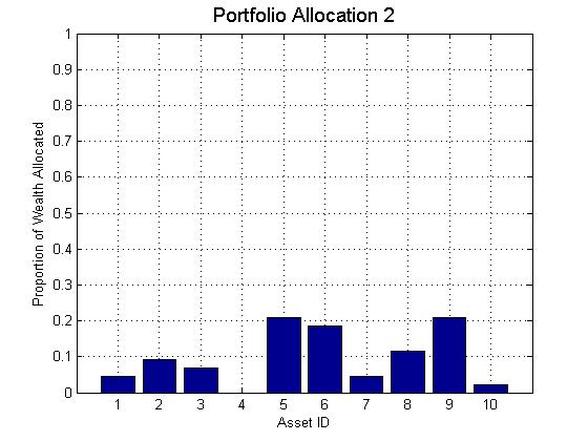
Assuming this is the portfolio held by the investor, after the end of a certain period (e.g. a day or a month), the investor's wealth will change according to the change in the price of the assets. After realizing this change (profit or loss), the investor will want to re-balance his portfolio, i.e., decide again what fraction of his wealth gets allocated to which asset. This is done on the basis of certain criteria, as determined by the investor. Let us assume the investor re-balances his portfolio to Portfolio Allocation 2, as shown below.
Assuming this is the portfolio held by the investor, after the end of a certain period (e.g. a day or a month), the investor's wealth will change according to the change in the price of the assets. After realizing this change (profit or loss), the investor will want to re-balance his portfolio, i.e., decide again what fraction of his wealth gets allocated to which asset. This is done on the basis of certain criteria, as determined by the investor. Let us assume the investor re-balances his portfolio to Portfolio Allocation 2, as shown below.
This new portfolio will now realize some profits/losses for the investor, and he will again make a decision to re-balance the portfolio.
Online Learning for Portfolio Selection
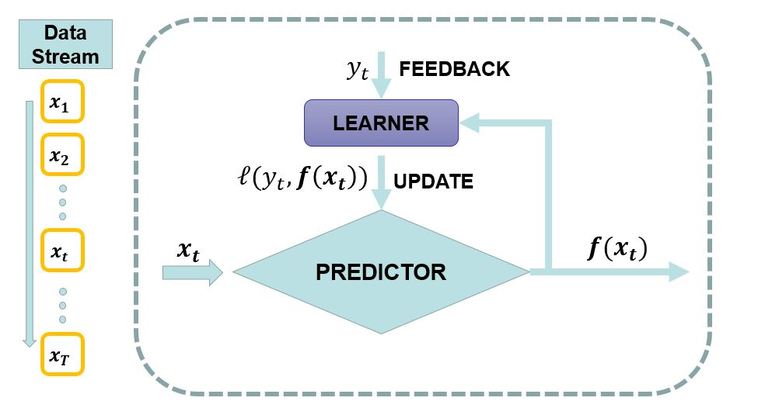
Online Portfolio Selection uses Online Learning Techniques to make portfolio allocation decisions. Online Learning Methods represent a family of scalable machine learning techniques. The generic framework for Online Learning can be seen below:
Online Portfolio Selection uses Online Learning Techniques to make portfolio allocation decisions. Online Learning Methods represent a family of scalable machine learning techniques. The generic framework for Online Learning can be seen below:
The key idea of online learning is that a model is learnt from a sequentially arriving stream of data. In every time step, an instance x(t) will arrive. The model makes a prediction. Based on this prediction (or decision), the model suffers a loss (usually a convex function). In an attempt to minimize future losses, the model makes an update.
Why is this relevant to portfolio selection? Because the problem setting of portfolio selection is a direct application on an online learning setting. In every period, the asset performances are revealed to the investor (equivalent of instance x(t)), and based on the portfolio held by the investor, a profit/loss is realized (which will help compute the <convex> loss function). This is followed by updating the portfolio (updating the model in online learning).
Why is this relevant to portfolio selection? Because the problem setting of portfolio selection is a direct application on an online learning setting. In every period, the asset performances are revealed to the investor (equivalent of instance x(t)), and based on the portfolio held by the investor, a profit/loss is realized (which will help compute the <convex> loss function). This is followed by updating the portfolio (updating the model in online learning).